number systems manipulation

수를 셀 때, 자릿수가 올라가는 단위를 기준으로 하는 셈법의 총칭으로 '위치적 기수법'이라고도 한다.
일반적으로는 10진법을 주로 사용하며, 시계는 12진법과 60진법의 조합, 컴퓨터에서는 2진법과 16진법 또는 3진법 등이 이용된다.
또한 암호학에서는 26진수가 사용되기도 한다.

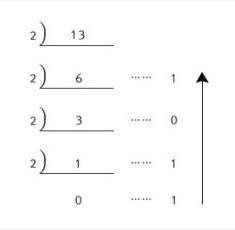
어떤 수를 n진법으로 변환하려면 그 수를 0이 될 때까지 n으로 나누고, 그 나머지를 거꾸로 읽어 올라가면 된다.

int(string, base)

의 형태로 작성한다. ex. 2진법 --> 10진법

print(int(10010, 2))

print(bin(number)[2:]) ### 2진법
print(oct(number)[2:]) ### 8진법
print(hex(number)[2:]) ### 16진법

결과는 모두 문자열로 출력된다.

다음은 16진법을 2진법으로 변환하는 과정이다.

import string
tmp = string.digits+string.ascii_lowercase
def convert(num, base) :
    q, r = divmod(num, base)
    if q == 0 :
        return tmp[r] 
    else :
        return convert(q, base) + tmp[r]
print(convert(int(a), 16), 2)

print(int(input(), 16))